Nodo artistico

In questo post e nel successivo, proverò a raccontare in termini non specialistici il mondo attorno a cui girerà la mia tesi di dottorato. Sono anch'io un assoluto novizio, quindi assicuro imprecisioni che spero siano mascherate dal contesto colloquiale. L'area della matematica in questione si chiama teoria dei nodi. Fortunatamente, è un settore molto meno astratto di altri. Sfortunatamente, non sono in grado al momento di descriverne applicazioni né al mondo reale né ad altre branche della matematica, sebbene ne esistano in quantità (quella narrativamente più fica pare sia in biologia molecolare). Magari in futuro.

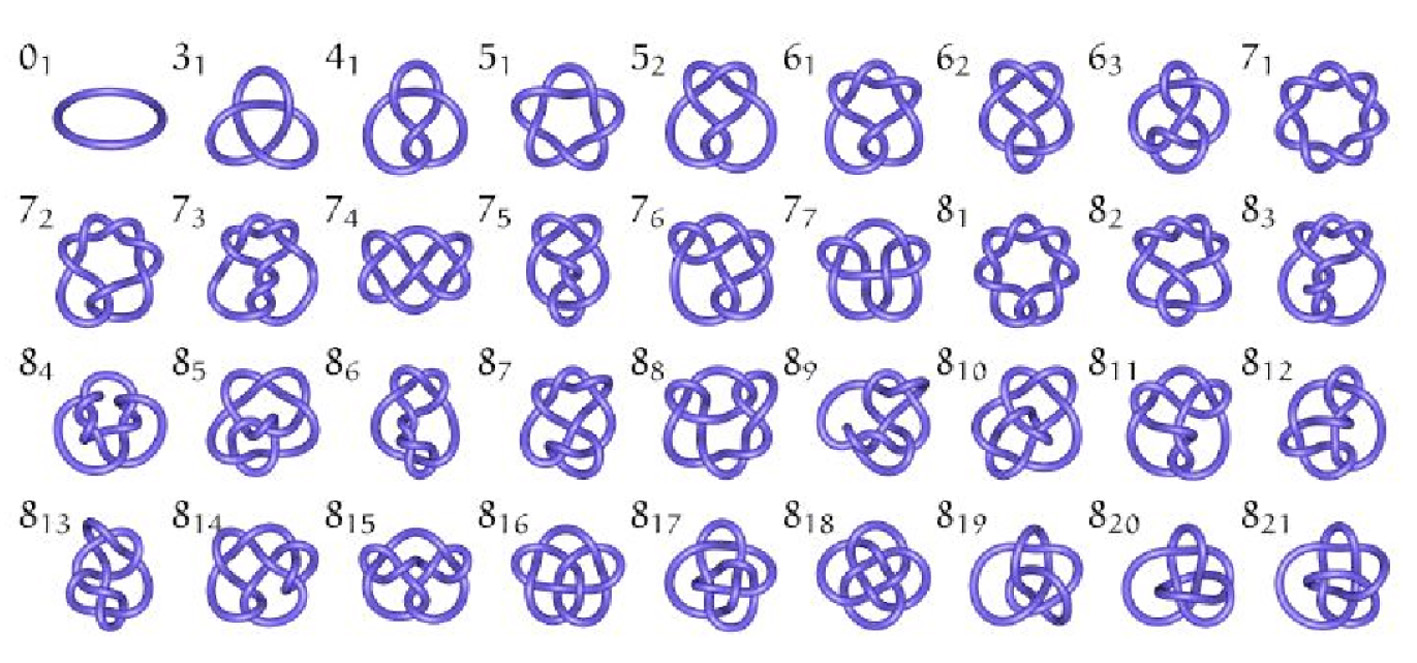
Un nodo, in matematica, è l'oggetto che si può ottenere prendendo un filo, intrecciandolo a piacimento e poi unendo le due estremità con una colla magica (giusto per evitare ulteriori attorcigliamenti). Ecco una tavola con alcuni tra i nodi più elementari.

Due nodi sono considerati uguali se i due fili possono essere portati nella stessa posizione senza effettuare tagli. Nella tavola di sopra i nodi sono esposti tramite proiezioni su un piano, in cui negli incroci si segnala quale segmento passa sopra e quale passa sotto. Uno stesso nodo può avere proiezioni molto diverse tra loro. Senza cercare complicazioni artificialmente create, ecco due possibili proiezioni per il nodo a trifoglio (destro), che si ottiene effettuando un nodo semplice e poi richiudendo le estremità del filo.

Uno degli obiettivi fondamentali della teoria dei nodi è quindi quello di creare degli strumenti per poter dire se, dati due nodi, essi sono uguali oppure no. Se si sospetta che i due nodi coincidano, si cercherà di trovare i giusti movimenti per trasformare l'uno nell'altro. Se si sospetta che i due nodi siano differenti, invece, bisognerà cercare una qualche proprietà (invariante rispetto a questi spostamenti nello spazio) che sia diversa per i due nodi. Molto spesso questa proprietà invariante è un numero o un oggetto algebrico più complicato.

E' chiaro che eventuali diversità tra due nodi non sono da cercare nel filo stesso, ma nel modo in cui esso è disposto nello spazio. Alcuni invarianti numerici possono essere definiti a partire dal diagramma delle intersezioni di una proiezione su un piano. Uno degli invarianti più semplici da definire (ma non da calcolare) è costituito dal minimo numero di "attraversamenti" - ossia, nei diagrammi di sopra, lo scambio di accavallamento in un'intersezione - necessario a trasformare un nodo nel nodo non attorcigliato. Ad esempio, per il nodo a trifoglio è sufficiente fare una mossa vietata di questo tipo per trasformarlo nel nodo non intrecciato.

Molto più spesso, però, la strategia adottata è quella di spostare l'attenzione dal filo stesso al mondo che gli sta attorno, facendo diventare quest'ultimo l'ente geometrico su cui lavorare. E' vero che modificando la disposizione nello spazio di un nodo anche il mondo che gli sta attorno sarà deformato, ma in una maniera dolce e continua che non ne varia la sua struttura più essenziale. Qui entra in gioco la topologia, ossia la disciplina che studia questa forma più essenziale degli oggetti, senza curarsi di queste eventuali deformazioni poco invasive. Per un topologo, un pallone da calcio sgonfio resta una sfera e una chitarra è uguale a un mandolino (a parte il numero di corde), ma i bucatini sono diversi dagli spaghetti. Di conseguenza, se gli spazi complementari a due nodi sono topologicamente differenti, non c'è speranza che un nodo si possa ottenere dall'altro senza effettuare tagli e reincollamenti.

Un risultato abbastanza recente ci assicura addirittura che questo passaggio al complementare nello spazio non fa perdere informazioni sul nodo in questione.

TEOREMA. (Gordon-Luecke, 1989) Se non rompi troppo le palle con casi patologici, lo spazio complementare a due nodi diversi è topologicamente diverso.

Un invariante per il nostro nodo può essere quindi definito attraverso la catena:

Nodo --> Spazio complementare X --> Invariante topologico associato a X.

Per rendere questo spazio complementare più maneggevole, si è soliti fare le due operazioni seguenti. Prima di tutto, invece di considerare il nodo come oggetto unidimensionale, si inspessisce il filo creandogli attorno un piccolo tubo che lo rende a tutti gli effetti tridimensionale, e si considera lo spazio complementare a questo oggetto di struttura simile ma dimensione diversa. Seconda cosa, si fa la follia di uscire dalla concretezza del nostro universo infinito a tre dimensioni e si vede invece il nodo come abitante in una sfera tridimensionale, o 3-sfera.

Che cos'è una 3-sfera? Non è un pallone da calcio, perché quando si parla di sfere si intende sempre il guscio all'esterno di una palla: un pallone è una 2-sfera, perché lo strato di cuoio è bidimensionale. Una 3-sfera non possiamo vederla perché non c'è modo di farla abitare in uno spazio tridimensionale, ma ragionando per analogia con gli oggetti analoghi di dimensione più bassa possiamo intuire com'è fatta. Una 1-sfera, ossia una circonferenza, può essere costruita a partire da un segmento (ad esempio un filo) in cui uniamo le due estremità, un po' come ho descritto all'inizio. Una 2-sfera può essere costruita a partire da un disco, che curviamo e chiudiamo facendo coincidere tutti i punti della circonferenza che lo circonda: a me viene da pensare al cappuccio di una felpa che viene stretto tirando i cordini. Una 3-sfera, quindi, può essere costruita a partire da una palla tridimensionale, piena anche dentro, che immaginiamo di richiudere in un mondo immaginario portando tutta la superficie esterna in un unico punto. Per farlo fisicamente avremmo bisogno di una quarta dimensione, ma studiarla come oggetto astratto è sempre possibile, e in questo caso il fine è avere informazione si oggetti concreti (i nodi).

Dicevamo, quindi, che vogliamo considerare i nostri nodi come immersi in una 3-sfera. Si tratta di una scelta sensata perché la teoria non cambia: due nodi sono equivalenti nello spazio tradizionale esattamente quando lo sono in una 3-sfera. Il vantaggio risiede nel fatto che lo spazio attorno al nodo diventa limitato e ci sono molti più strumenti per studiare le forme di questo tipo.

A titolo di esempio, proverò da qui alla fine a descrivere lo spazio attorno al nodo più banale di tutti, quello in cui il filo non è stato intrecciato per niente, facendo vedere che in realtà esso ha una forma che già conosciamo. Come già detto, prima di tutto costruiamo attorno al nostro nodo un piccolo tubo, che in questo caso avrà la forma di un tarallo. Dopodiché, possiamo pensare di immergere questo tarallo in una palla piena e far collassare la superficie esterna in un punto (se non ve ne eravate accorti, siamo entrati da un pezzo nella parte del talk in cui non si capisce più niente).

ESEMPIO. Lo spazio attorno a un tarallo non è che un altro gigantesco tarallo. 

(Per il teorema di Gordon-Luecke, ne segue che se mostriamo che spazio attorno a un nodo ha la forma di un tarallo, allora quel nodo è necessariamente il nodo banale. E non è sempre facile capirlo a prima vista.)

Per illustrare questo fatto a prima vista sorprendente, proverò a fare un disegno in vari colori. Tracciamo in blu il nostro tarallo, all'interno di una palla rappresentata in nero. Ricordo che tutto il bordo di questa palla è in realtà da considerarsi un unico punto, indicato con il simbolo ∞. Vogliamo mostrare che l'esterno di questo tarallo ha ancora la forma di un tarallo. Ma com'è fatto un tarallo? Che i panettieri pugliesi lo sappiano o meno, un tarallo è costituito da un'infinità di dischi posti uno accanto all'altro a girare attorno al buco centrale. Disegnerò questi dischi in verde (ma solo due, che sennò non si capisce niente), e le circonferenze trasversali, che fanno il giro del buco, in rosso. Ok, mi accorgo ora che i colori si vedono malissimo, ma non è facile qui trovare una giornata luminosa!

Quella che sembra una corona (verde), è in realtà un disco, centrato nel punto ∞. Analogamente, il segmento rosso è da pensare come una circonferenza, che passa per 0 e per ∞. Facendo collassare tutto il bordo della palla a un punto e rigirando l'interno con l'esterno, il complicato disegno fatto sopra diventa una cosa del genere. La curvatura un po' strana e asimmetrica deriva dal fatto che stiamo forzando in uno spazio tridimensionale un oggetto che vivrebbe più volentieri in dimensione 4. Ma già siamo fortunati che questo sia possibile, per cui non ci lamentiamo.

Per capire meglio cosa sta succedendo, è utile dare un'occhiata alla situazione analoga in una dimensione minore. In questo caso, l'oggetto finale è una superficie in uno spazio tridimensionale, e non sarebbe nemmeno possibile farlo abitare in due dimensioni.

Concludo con una tipica barzelletta.

- What area of maths do you like most?
- Knot theory.
- Yeah, me neither.